|
Digitale Schaltungen - selbst erstellen |
Man könnte sagen: "Das ist Teil2 der Digitalen Schaltungen!"
Damit will ich sagen:
- Es gibt schon einen Teil zu Digitale Schaltungen
- Den Teil sollte man schon absolviert haben!
Ziel dieses Teils ist, aus einem irgendwie beschriebenen technischen Problem eine Schaltung zu entwickeln!
Dazu gehen wir in folgenden Schritten voran:
- Beschreibung des Problems verbal / technisch
- eine entsprechende formulierung finden (Formel)
- Vereinfachungen finden und anwenden
- Schaltung aufstellen
- bestimmte Sorten von Bauelementen nutzen
Weiterhin soll in diesem Teil die Art der digitalen Schaltungen auf solche ohne
Speichereigenschaften beschränkt werden.
Allerdings werden wir das Vereinfachen und das Erstellen der Schaltung hier schon
mal intensiver behandeln, es gilt ja auch für andere Arten der digitalen Schaltungen.
Verbale Beschreibung des technischen Problems
"Ich will mal einen Computer bauen!" - na ja, das wird wohl nichts werden!
Aber Teile daraus gehen:
-
"Ich will für einen Computer ein Addierwerk bauen zur Addition von ganzzahligen Werten"
Jeder Taschenrechner kann bereits mit Komma oder mit Zehnerpotenzen rechnen, so
1.2345 1031,
das kriegen wir nicht so ohne weiteres hin
Man muß sich aber auch einmal überlegen, was diese Größe aussagt. Mit einem Maßstab von
1 : 1022
kann man bereits unsere gesammte Galaxis darstellen - 1031 kann nur noch eine Rechengröße sein:
-
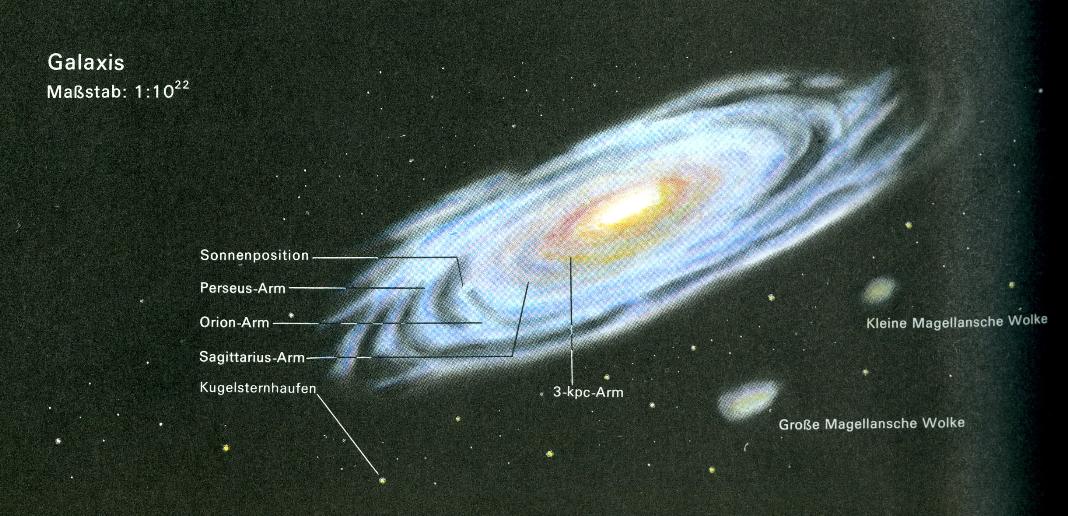
(aus Meyers neues Lexikon, 1978, VEB Bibliographisches Institut Leipzig)
ok - wir bleiben bei dem kleinen Addierwerk. Aber schon gibt es neues Problem -
wie rechnet eigentlich so ein Computer?
Man spricht ja auch genauer von einem Digital-Rechner.
Und da sind wir wieder bei digital.
Das bedeutet ganz einfach gesagt, dass wir nur die Zahlen (besser: Ziffern) 1 oder 0 zur Verfügung haben.
Was wir brauchen, ist ein kleiner Exkurs zu Zahlensystemen:
-
Wir denken zumeist im Dezimalzahlensystem. Schreiben wir 123 auf, weiß jeder, dass
Ein Hundert Drei und Zwanzig gemeint ist, d.h. man ordnet ganz automatisch den Ziffern
einen Wert zu (1 Wert 100, 2 - Wert 10, 3 - Wert 1).
Der Wert richtet sich nach der Position der Ziffer. Deswegen kann mann
das Problem auch so formulieren:
-
1 x 102 + 2 x 101 + 3 x 100 = 123
(102 = 100, 101 = 10, 100 = 1)
Wir übermitteln nur die Ziffern, die Stellenwerte ordnet jeder selbst zu.Die 10 in diesem System kennzeichnet das "Dezimalsystem", also können wir auch ohne Probleme ins Dualsystem umschwenken. Es muss ja gelten:
-
... + 1/0 x 22 + 1/0 x 21 + 1/0 x 20 = Dualzahl
(1/0 - es können die Ziffern 1 oder 0 verwendet werden)
Aber wir haben nun ganz andere Stellenwerte:- 22 = 4, 21 = 2, 20 = 1 (wir können froh sein, dass die kleinste Stelle wieder 1 ist)
Schreibt man also im Dual-System auf:- 1011 = 1011(2), so ist das: 1 x 23 + 0 x 22 + 1 x 21 + 1 x 20 = 8 + 0 + 2 + 1 = 11(10)
Wir wollen uns angewöhnen, wenn die Zahl nicht so eindeutig ist, in Klammern die Basis hinter zu schreiben, (10) - Dezimalzahl, (2) - Dualzahl. -
1 x 102 + 2 x 101 + 3 x 100 = 123
Aufgabe1:
Ermittle aus den Dezimalzahlen: 3, 7, 81 und 123 die Dualzahlen!
(erst einmal probieren, dann später hier nachsehen)
-
Die nächste Frage ist nun, wie man im Dualsystem rechnen kann?
Ganz einfach - genau wie im Dezimalsystem!
Natürlich muss man das mal wieder "zu Fuß", also per Hand ohne Taschenrechner erledigen.
Man beginnt von rechts mit der niederwertigsten Stelle und arbeitet sich Stelle für Stelle nach links durch und das auch unter Berücksichtigung der Überträge! Also dezimal z.B.:-

Von rechts beginnend, ist
3 + 7 natürlich 10 (der Übertrag ist in der ersten Stelle natürlich 0),
wir schreiben aber nur die 0 hin, aber einen Übertrag für die nächste Stelle!
In der nächsten Stelle müssen wir nun auch den Übertrag mit berücksichtigen:
2 + 5 + 1 = 8
Der Übertrag für die nächste Stelle ist 0. In der dritten Stelle gilt
1 + 0 + 0 = 1 (die erste 0 kommt aus der zweiten Zahl)
Noch ein anderes Beispiel:-

Der wesentliche Unterschied zum verhergehenden Beispiel ist, daß in der letzten Stelle ein Übertrag entsteht - im Ergebnis erweitern wir einfach den Wert um eine Stelle nach links, wenn das Papier auf dem wir schreiben noch links Platz hat, geht das.
Aber wir haben eben ein kleines wenn gehört!
Nun soll das auch im Dualsystem versucht werden:-

Man kann das auch im Dezimalsystem verfolgen, wir addieren 11(10) + 3(10),
das sollte 14(10) als Ergebnis bringen.
Dual funktioniert das in gleicher Weise
rechte Stelle:
- 1 + 1 + 0 = 0 => Übertrag 1 in die nächste Stelle,
- 1 + 1 + 1 = 1 => Übertrag 1 in die nächste Stelle,
- 0 + 0 + 1 = 1 => Übertrag 0 in die nächste Stelle,
- 1 + 0 + 0 = 1 => kein Übertrag
Als Ergebnis entsteht 1110(2) das entspricht natürlich 14(10).
Nun auch noch das zweite Beispiel in dual:-

Nun haben wir ein kleines, nein ein großes Problem, das "wenn" von oben gilt, wir haben kein Platz mehr.
Wenn man sich technisch auf 4 Stellen festgelegt hat, geht es eben nur mit 4 Stellen - wir müssen überlegen, was man mit dem Übertrag machen kann!
Auch wenn man die Stellenzahl erhöht, irgendwann geht es nicht mehr. In der Technik ist man so bei 64 Stellen.
Soviel zu unserem kleinen Ausflug in Zahlensysteme. -
Zur weiteren Bearbeitung treffen wir die Festlegung:
- 1. Wir konstruieren ein Addierwerk mit maximal 4 Stellen.
Die nächste Frage ist: "Was machen wir mit Kettenrechnungen?"
Also, so etwa:
2 + 3 + 1 + 5 + 1
Die nächste Forderung sind 33 Summanden usw. Nicht für jede Anordnung kann man ein
Addierwerk bauen, man muß eine allgemeingültige Regel finden!
Eine solche wäre z.B.
Zwischensumme i-1 + Summand i = Zwischensumme i
also die neue Zwischensumme ist die Summe aus alter Zwischensumme plus neuem
Summand
Das bei dieser Aktion nicht nur 2 Summanden sondern auch der Übertrag verarbeitet
werden muss, wissen wir schon. Das Ganze kann man nun beliebig
oft wiederholen, man muss nur die richtigen Summanden ran-organisieren.
Und dann bleibt noch die Frage nach der Zwischensumme am Anfang? Die setzen wir
einfach auf 0 (jede Stelle 0). Hier mal so ein Beispiel:
Wir brauchen also zur Lösung des Problems nur das gekennzeichnete Kästchen zu realisieren!
|
Und da wir nun auch schon wissen, dass die Rechnung Stelle für Stelle erfolgt, braucht zunächst nur eine Stelle konstruiert werden! |

|
Damit können wir eine nächste Festlegung aufstellen:
- 2. Wir konstruieren einen Addierer der 3 Eingänge: S1, S2, Ü und 2 Ausgänge: S, Ü haben muss.
Symbolisch könnte das so aussehen:
Bauen wir 4 davon nebeneinander auf, haben wir unser kleines Addierwerk:
Würden wir davon 16 Stück aufbauen, hätten wir ein Addierwerk von 16 x 4 = 64 Stellen, das ist genau die Größe in einem modernen Computer.
Das wird uns sicher nicht gelingen - wir konzentrieren uns lieber nur auf eine Stelle!
Eine Bemerkung ist jedoch notwendig:
Würde man so ein Addierwerk für einen 64 Bit (Verarbeitungsbreite) Rechner aufbauen, so würde er zu langsam arbeiten, denn die 64-ste Stelle ist erst richtig wenn die 63-ste Stelle ein Ergebnis bringt (in S und Ü geht immer die Vorstelle mit in die Berechnung ein), die 63-ste nach der 62-sten usw. Erst nachdem das 63 mal passiert ist, hat man ein richtiges Ergebnis - das ist zu langsam, daher gibt es auch noch andere Lösungen, das lassen wir aber!
Wir wiederholen noch einmal:
-
Unsere verbale Aufgabenstellung lautet:
Bau einer digitalen Schaltung zur dualen Addition einer Stelle:
S = S1 + S2 + Ü
Ün = Fkt(S1,S2,Ü) (der neue Übertrag wird aus den Werten S1, S2 und Ü errechnet)
Technische Beschreibung des Problems
Aus
Teil1 der digitalen Schaltungen
wissen wir, dass man das logische Verhalten einer Schaltung sehr gut durch eine
Wahrheitstabelle beschreiben kann.
Das Verfahren drehen wir nun einfach um - wir erstellen als erstes eine Wahrheitstabelle,
dazu muss es mindest eine Schaltung geben.
Wir haben 3 Eingangsgößen für die Schaltung, also muss die Wahrheitstabelle auch 3 Variable
haben, die die Werte 0 und 1 annehmen können. Die Kombination gibt dann 8
Möglichkeiten:
Mit dem oben schon gezeigten Verfahren müssen wir nun herausfinden, bei welcher Kombination gibt es einen Übertrag und wie groß ist die Summe für jede Kombination der Eingangsgrößen.
-

Wenn eine 1 in der Kombnation auftritt, ist die Summe 1 und der Übertrag 0.
Tritt die 1 zweimal auf (egal wo, Ü oder a oder b), dann ist die Summe 0 und der Übertrag 1.
In der letzten Kombination ist dann sowohl die Summe, wie auch der Übertrag 1.
Wir wollen das noch einmal deutlich kennzeichnen:
-

Es gibt also sowohl für S als auch für Ü nur an bestimmten Stellen eine 1. Das wäre dann wie im Teil1, wenn die LED leuchtet - nur das interessiert uns!
Man könnte also sagen, dass die LED für die Summe leuchtet,
wenn Ü = 0 und b = 0 und a = 1 ist oder wenn Ü = 0 und b = 1 und a = 0 ist oder ...
Ein wenig verändert (Aussagen auf 1 bezogen):
wenn Ü ungleich 1 und b ungleich 1 und a gleich 1 ist oder wenn Ü ungleich 1 und b gleich 1 und a ungleich 1 ist oder ...
Das kann mann verallgemeinern und schreibt für die Summe:
also: (nicht Ü UND nicht b UND a) ODER (nicht Ü UND b UND nicht a) ODER (Ü UND nicht b UND nicht a) ODER (Ü UND b UND a)
So kann man natürlich auch den Übertrag aufschreiben:
Solche einfache Simulatoren kann man aus dem Netz laden, z.B. den DigitalSimulator 5.57:
In dem Simulator gibt es bereits genau so ein Bauelement zur Addition. "Zusammengesteckt" ergibt sich folgendes Bild:
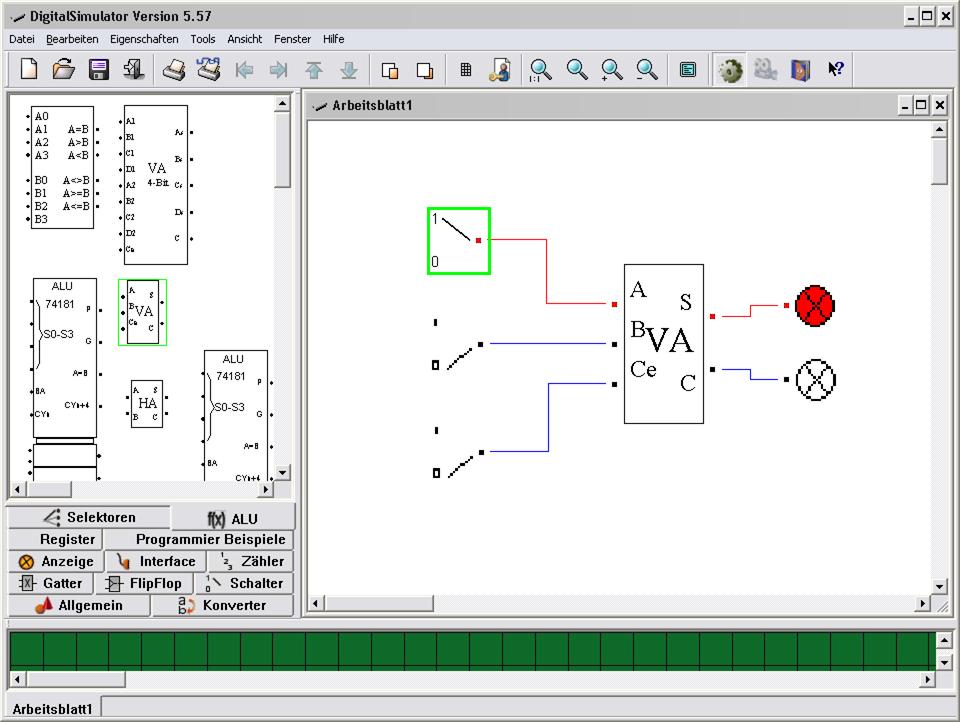
Im linken Fenster gibt es eine Auswahl der Bauelemente. Es wurde "f(x) ALU" und in dem
Angebot dann VA (VollAdder)ausgewählt. Das Element wird wie üblich mit
der Maus angeklickt und rübergezogen. Aus dem Angebot "Schalter" kommen die Schalter
und aus "Anzeige" die Lampen. Verbindungen der Elemente werden einfach durch ziehen
mit der Maus vom Ausgang zum entsprechenden Eingang organisiert usw.
Im übrigen lassen sich fast alle Bauelemente noch modifizieren. Nach Klicken aufs
Zahnrad in der Bedienleiste sind die Schalter aktiv und schalten durch Anklicken um -
ich finde das einfach toll.
Das Bild zeigt A = 1, B = 0 und C (Ü) = 0, daraus folgt S = 1 und C (ü) = 0;
obere Lampe für die Summe leuchtet (1), die untere nicht (0).
Die Datei: digitalsimulatorv5.57.exe muss man aus dem Netz laden (etwa 27MB).
Viele Uni's verwenden diese Software, kann man dort herunterladen
(Niemals Adresse angeben, ist Free-Ware - dann ist es ein unlauterer Anbieter!).
Man muss zur Installation als Administrator angemeldet sein und eine Internetverbindung
haben. Bisher habe ich auch keine Vieren über die Seite abgefasst, dass das so immer
ist -
-
dafür übernehme ich keine Garantie!
Auch die Nutzung des Simulators erfordert Administrator-Rechte.
Aufgabe
Zur Festigung und Kontrolle wollen wir eine zweite Aufgabe als Übungsaufgabe bearbeiten, d.h. ich weniger!
Im Teil1 der digitalen Schaltungen
haben wir die logischen Grundfunktionen wie AND, OR, NAND und NOR kennengelernt.
Wir wollen nun eine Schaltung (Schaltkreis) entwickel, die alle 4 Grundfunktionen
ausführen kann!?
Hinweise:
Es sollen nur 2 Eingänge logisch Verknüpft werden.
Da 4 Funktionen dazu ausgewählt werden sollen, braucht man 2 weitere Eingänge:
- z.B. S1: 0 - AND; 1 - OR; S2: 0 - unnegiert; 1 - negiert
Die Wahrheitstabelle könnte dann etwa so aussehen:
-
S1 S2 a b | y | Funktion
-----------------------------------
0 0 0 0 | |
Aufgabe2
Vervollständige die Tabelle mit allen Kombinationen der 4 Eingangsgrößen und trage unter
y das logische Ergebnis ein.
Unter "Funktion" ist der Name der aktuellen logischen Funktion einzutragen.
(erst einmal probieren, dann später
hier nachsehen)
Vereinfachung der Beschreibung per Formel
Nun haben wir die Beschreibung der Schaltung mittels einer Formel. Daraus kann man
sofort die Schaltung erstellen - das heben wir uns aber noch etwas auf, denn man
sollte immer zunächst mal schauen, ob die Formel vereinfacht werden kann.
Das ist ganz wichtig, denn jede Verkleinerung der Formel reduziert auch die
Schaltung, d.b. weniger Gatter - weniger teuer. Das schränkt nicht die Funktion ein,
es werden nur unsinnige Verbindungen und logische Funktionen gesucht und beseitigt.
Die Basis der Arbeit sind die schon aus Teil1 bekannten Regeln:
Eine weitere Möglichkeit besteht im "Ausklammern". Das sieht dann z.B. so aus:
-

Bisher wurde es nicht so deutlich gesagt:
AND hat höhere Priorität als OR
deshalb müssen die Klammern geschrieben werden!
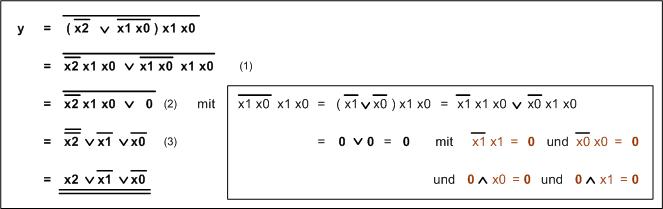
Mit dem Wissen können wir uns nun einmal an einer größeren Formel versuchen:
Man muss solche Formeln zunächst erst einmal in Ruhe betrachten und analysieren. Wir stellen fest:
es gibt 3 Eingangsgrößen: x2, x1, x0
das Darstellen als Schaltung ist sicher noch nicht sinnvoll - wir sollten vereinfachen!
Im ersten Schritt (1) beseitigen wir erst mal die Klammer.
Der letzte Teil mit x1 und x0 einmal negiert und einmal nicht, ist immer sehr
verdächtig für eine dolle Vereinfachung.
In dem Extra-Kästchen soll das probiert werden:
Zunächst beseitigt man die Negation über die beiden Werte, erhält die Negation der
einzelnen Werte und das logische ODER.
Jetzt kann man wieder die Klammer beseitigen und erhält zwei Ausdrücke in denen die eine
Größe immer negiert und unnegiert auftritt. Das ist gut denn dass ist 0. Aber 0 UND x
ist auch 0, damit wird tatsächlich der ganze Teil 0 (2).
Nun kann man den langen Strich beseitigen (3) und erhält ein relativ einfaches Ergebnis.
Es hat sich doch gelohnt, hier zunächst theoretisch an der Formel zu arbeiten,
wir brauchen nur noch einen ODER-Baustein mit 3 Eingängen und 2 Negatoren (sicher ein
zweiter Baustein - geht aber auch mit nur einem).
Das Kästchen muss man noch einmal betrachten:
-

Wenn man das als Schaltung aufbauen soll, kann man sich viel Arbeit machen.
Wir haben aber gezeigt dass das Ergebnis 0 ist!
Was bedeutet das?
Die Schaltung funktioniert wie eine Leitungsunterbrechung, ich kann sie auch weglassen!!!
So spart man also noch mehr Aufwand.
Nun tausche wir in der Formel einfach mal ein Rechenzeichen um:
-

Die Vereinfachung (1) ist zu verstehen.
In (2) kommt jedoch ein fieser Trick, wir fügen zu x1 negiert einfach mit UND eine 1 hinzu - das ist ok. Daneben steht wie die 1 realisiert wird, dass ist auch richtig, aber wer kommt darauf?
In (3) wird das eingesetzt, und in (4) ausgerechnet, was dann in (5) wieder anders ausgeklammert wird - und siehe da, da x ODER x negiert 1 ist und auch x ODER 1 auch 1 ist bleibt nur x ODER x negiert (6), das ist aber auch 1, was nun auch das Ergebnis ist!
Was bedeutet das?
Die Schaltung funktioniert nun wie ein Draht, kann man also weglassen und die Betriebsspannung an den nächsten Eingang legen!!!
Was kann man aus den Beispielen sehen
- Vereinfachen lohnt sich!
Das wollen denn auch gleich einmal üben.
Aufgabe3:
Vereinfache folgende Schaltfunktion:
(erst einmal probieren, dann später hier nachsehen)
Das Vereinfachen der Funktionen für das Addierwerk und das Universalgatter verschieben
wir auf den nächsten Punkt. Beide lassen sich wenig vereinfachen und das nur wieder
durch hinzufügen weiterer Elemente - also später!
Fakt ist, dass es einiger Übung bedarf immer den richtigen Ansatz zu finden!
Vereinfachung der Beschreibung per Grafik
Basis für eine Vereinfachung war das Ausklammern:
Der Teil in der Klammer wird 1 und 1 UND "Irgendwas" ist das "Irgendwas", in diesem Fall also a.
Wenn man nun diese beiden Ausdrücke so grafisch anordnet, dass sie nebeneinander stehen, dann wird sofort ersichtlich, dass genau b herausfällt. Zunächst einmal ist klar, dass es noch 2 weitere Kombinationen aus a und b gibt. Komplett sieht das so aus:
Die Teile
Diese Teile können nur fehlen, wenn ihr Wert 0 ist, denn 0 ODER "Irgendwas" ist "Irgendwas". Um Kombinationen mit 2 Variablen komplett darstellen zu können, brauchen wir 4 Felder. Folgende Möglichkeit besteht:
-


Die Anordnung der 4 Elemente ist beliebig, es sollte jedoch ein Quadrat sein und einer Regel entsprechen:
Die Elemente dürfen sich nur in einer Stelle unterscheiden!
In der oberen Zeile ändert sich nur die rechte Stelle, genialer Weise auch in der zweiten Zeile
Auch unterscheidet sich die zweite Spalte nur um eine Stelle von der ersten Spalte.
Bei größeren Anordnungen gilt die gleiche Forderung.
Gibt es also benachbarte Elemente, fällt diese Stelle heraus! - das entspricht genau der beschriebenen Vereinfachung.
Die Elemente können nun auch so beschrieben werden.
Das Element unten links,
Man kann auch die zugehörenden dezimalen Werte ausrechnen und die Kästchen so beschriften:
-


Häufig sieht man, dass nur die unnegierten
Bezeichnungen der Spalten und Zeilen geschrieben
werden.
-
Nehmen wir folgendes Beispiel:

Diese beiden Teile tragen wir ins Schema
ein bei 3 und 1, sie sind benachbart.

Und so kennzeichnet man diese Gruppe, sie liegt komplet in a (b ist einmal negiert und einmal unnegiert - fällt also raus).
Das Ergebnis ist somit: y = a
-
Ein anderes Beispiel:

(das erste Element (1) liegt oben links (nicht in b und nicht in a),
das zweite (1) oben rechts (nicht in b aber in a),
das dritte (2) unten links (in b nicht in a).
Es sind zwar 3 benachbarte Elemente aber "um die Ecke", das geht nicht. Und 3 Elemente schon gar nicht.
Unser Ansatz war, dass wir aus zwei Elementen eine Größe ausklammern, also geht das hier wie überhaupt bei drei Elementen nur mit zwei Blöcken. Das sollte man sich merken:
Vereinfachen kann man nur Blöcke mit 2i i = 1,2,3,4,5,6 Elementen, also 2,4,8,16,32,64
Als Ergebnis erhalten wir:
Per Formeln wäre wieder der Trick des Hinzufügens eines Ausdrucks notwendig gewesen.
Noch ein letztes Beispiel, bevor wir uns wieder unserer Aufgabe widmen:
-

Das scheint irgendwie unsinnig zu sein, das entspricht der schon bekannten Funktion:

Wenn alle Elemente herausfallen entspricht das wieder einem Draht,
das Ergebnis ist 1.
Unsere Aufgabe war, von einem Addierwerk die Schaltung für eine Stelle zu entwickeln. Die Wahrheitstabelle und die Funktionen haben wir schon erarbeitet. Nun steht die Frage, ob hier eventuell etwas vereinfacht werden kann. Wir wollen dazu wieder das grafische Verfahren bemühen.
Mit 3 Variablen kann man 8 Kombinationen erzeugen, die müssen wieder sinnvoll angeordnet werden, ein Quadrat geht nicht. Aber auch im Rechteck gibt es Möglichkeiten die Kombinationen so anzuordnen, dass sie sich zum Nachbarn immer nur in eine Stelle unterscheiden, es gibt viele Varianten. Ich schlage folgende vor:
-

Man beachte, dass auch die rechte Spalte auch an die ganz linke passt, d.h. es kann auch Blöcke über die Ränder hinweg geben!
Auf unsere Aufgabe bezogen und mit der Schreibweise, dass a und b genau auf einen Trennstrich zeigen, das soll bedeuten, dass links und rechts davon die Spalten unnegiert sein sollen. So das nächste Bild:
Man kann auch wieder die dezimalen Werte ausrechnen und für diese Anordnung nutzen:
-
Tragen wir nun die Summe in das Schema ein:

dann entsteht folgendes Bild, was wieder typisch ist.
Es entsteht so eine Art kleines Schachbrettmuster. Dazu gibt es sofort zwei Aussagen:
- das kann man nicht vereinfachen
- das ist die typische Darstellung für XOR
Also keine Vereinfachung, damit müssen wir die Summe konstruieren.
-
Probieren wir das gleiche mit dem Übertrag:

dann läßt sich etwas vereinfachen.
Die linke wagerechte Kombination liegt in b und Ü, a fällt raus,
die rechte wagerechte liegt in a und Ü, b fällt raus,
die senkrechte liegt in a und b, Ü fällt raus, also ist das Ergebnis nun:
- Ün = Ü b oder Ü a oder b a
Die erste Aufgabe ist nun bezüglich der Vereinfachung abgearbeitet, nun wollen wir uns wieder dem universellen Baustein für die logischen Grundfunktionen zuwenden.
Auch hier soll nun eine grafische Vereinfachung realisiert werden.
Man sieht sofort, dass es wohl schwieriger werden wird, denn nun haben wir es mit
4 Eingangsgrößen zu tun - aber keine Bange, das packen wir auch!
Wie bisher gilt auch hier die Forderung, die Elemente so anzuordnen, dass sie sich zum Nachbar nur um eine Stelle unterscheiden. Das klingt erstmal schwierig, wir erweitern aber nur das Schema für 3 Größen, indem wir zwischen die zwei Zeilen zwei weitere einfügen. Für allgemein genannte Größen dcba kann man leicht folgendes Schema aufschreiben:
Die Größen a und b sind wie bisher für die Bezeichnung der Spalten zuständig, c und d nun für die Zeilen. Da es nun 16 Kombinationen aus den 4 Größen gibt ordnet man sie wieder zum Quadrat an und man kann natürlich auch mal die Dezimalwerte berechnen und eintragen:
(Es geht immer von außen nach innen, von links nach rechts und von oben nach unten)
Man kann selbstverständlich auch eine andere Anordnung finden, das ist völlig egal,
man sollte nur ein Schema nutzen, was man sich leicht merken kann.
Noch etwas ist zu beachten:
- Alle Elemente müssen immer durch alle Größen (Variable) beschrieben werden!
Ist das nicht der Fall, muß man die entsprechend fehlende Größe hinzufügen - nicht so, sondern nach den Regeln:
- abc UND 1 mit 1 = d ODER d negiert => abcd ODER abcd(negiert)
Nun gibt es große Blöcke, ein 16-er Block ist wieder ein Draht. Man sollte immer
große Blöcke finden, jede 1 muß mindest einmal durchlaufen werden.
Nehmen wir ein Beispiel:
Wir berechnen die Werte der Kombinationen und tragen diese ins Schema ein.
-
Werte: 2,1,12,15,13,4,5 
-
Dieses Element
ist einzutragen:


nicht in a
(1. und 2.
Spalte)
UND
in b
(2.Spalte)
UND
nicht in c
(2.Spalte
1. und 2.
Zeile)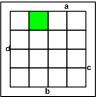
UND
nicht in d
(2.Spalte
1.Zeile)
Oder man trägt eine 1 an der Position 2 ein (das Element hat den Wert 2 s.o.)
Insgesamt haben wir nun 7 mal eine 1 im Schema. Auf den ersten Blick sieht man 3 zweier
Blöcke und 2 einzelne Elemente.
Ich möchte noch einmal an die Möglichkeit erinnern, dass es auch über den Rand hinaus
weiter geht - nun der zweite Blick und wir stellen fest, es gibt sogar einen 4-er
Block (unten links und rechts) und das obere rechte Element bildet nach unten ein
2-er Block. Das Element, was als Beispiel gezeigt wurde (die 2), bleibt ein einzelnes
Element. Damit gibt es nun folgende Blöcke:
Folgende Vereinfachungen sind nun möglich:
(Die kleinen roten Zahlen stehen für den Block im Schema)
Es gilt also:
-
der 4-er Block liegt komplett in c und komplett nicht in b, also
c UND b(neg)
in d und a liegt er teils teils - fallen raus -
der 2-er Block liegt in a in c und in d,
d UND c UND a
(b fällt raus) -
der 2-er Block liegt nicht in d, nicht in b, aber in a,
d(neg) UND b(neg) UND a
(c fällt raus) -
der 1-er Block muss wie gehabt aufgeschrieben werden
liegt nicht in d, nicht in c, in b, nicht in a
d(neg) UND c(neg) UND b UND a(neg)
(es fällt nichts raus)
Wir können feststellen, dass es eine recht große Vereinfachung gab!
Dieses Ergebnis könnte man nun in eine Schaltung umsetzen
Zuvor gibt es jedoch eine Aufgabe, denn unser Universal-Baustein (4 logische Funktionen)
muss auch noch bearbeitet werden.
Aufgabe4:
Für den Universalbaustein mit 4 logische Grundfunktionen, kann man aus der Wahrheitstabelle folgende Funktionsbeschreibung aufstellen:
Diese Formel wollen wir mittels grafischem Schema vereinfachen!
(erst einmal probieren, dann später hier nachsehen)
Eigentlich ist das ganz einfach, denn wir haben ja die Beschreibung durch die Formel, die brauchen wir ja nur umsetzen. Nehmen wir wieder als Beispiel unseren Addierer:
Ganz allgemein müssen wir aus den notwendigen Eingängen alle entsprechenden logischen Verknüpfungen aufbauen:
Man sieht schon, dass bereits zwei UND-Teile erhebliches Durcheinander bedürfen - das müssen wir ändern.
Da die Struktur der Formeln eigentlich immer gleich ist, kann man nach einem Schema verfahren:
Wir beginnen in einer Ecke, z.B. oben links, führen die ersten logischen Operationen aus und stellen diese über Leitungen bereit.
Von diesen "Zwischenergebnissen" bilden wir erneut die nächsten notwendigen logischen Verbindungen, stellen die Ergebnisse wieder über Leitungen, aber senkrecht zu den alten, zur Verfügung. Dabei ist die Richtung egal, hauptsache senkrecht zur vorhergehenden.
Und siehe da, unsere Schaltung wird übersichtlich (Addierer)!
Schaltung Addierer
Diesmal wurde unten rechts begonnen, dies aber nur um die Ein- und Ausgänge mit dem Addierer-Symbol etwa in Übereinstimmung zu bringen.
Die ersten Aktionen ist die Negation jedes Signals, daraus werden 8 Leitungen angeboten (logisch - wenn die Negation nicht gebraucht wird, braucht man sie auch nicht zu erzeugen). Von diesen nimmt man für jeden UND-Block die Signale ab. Der nächste Schritt bleibt in gleicher Richtung, da diese Signale nur einmal gebraucht werden, ansonsten wieder nach links die entsprechenden Kombinationen.
Auch die Kontrolle der Funktion ist relativ einfach, denn in den UND-Blöcken brauch nur eine Leitung mit 0 auftreten, dann ist ja das Ergebnis des Blockes auch 0 und bringt für das folgende ODER keinen Beitrag. Im Beispiel wurde der Fall a = b = 1 untersucht. Das Ergebnis entspricht der Theorie: Ün = 1 und S = 0.
Das können wir denn mal üben.
Aufgabe5:
Für unseren Universalbaustein zur Realisierung von 4 logischen Grundfunktionen sollte folgende Formel nach der Vereinfachung entstanden sein:
-

(die roten Zahlen entsprechen den Vereinfachungsblöcken)
Erarbeite für diese Funktion entsprechend dem beschriebenen Schema die Schaltung!
(erst einmal probieren, dann später hier nachsehen)
Umwandlung der Schaltung in eine bestimmte Gatter-Form
Das kann durchaus passieren - auf Grund von irgendwelchen technischen Forderungen,
sei es dass nur diese Sorte Gatter vorhanden ist oder die billiger sind, ist eine
bestimmte Gatter-Art gefordert.
Wir legen mal fest: "Wir wollen nur NAND-Gatter mit zwei Eingängen verwenden!!!"
Ich gebe zu, das ist heftig, aber es geht. Auch hier gibt es systematische Schritte,
die die Aufgabe vereinfachen oder erst möglich machen. Zwei Möglichkeiten sind
vorhanden:
-
Bearbeitung der Formel
Diese Variante geht von der Theorie der Schaltalgebra aus und erfordert einige Kenntnis und noch viel mehr Erfahrung! -
Experimentelles Einsetzen der Ersatzlösungen -
das ist für uns sinnvoll!
Wir haben im Teil1 bereits kennengelernt, dass jede logische Schaltung durch NAND's oder NOR's realisierbar ist. Unsere verschärfte Forderung war aber noch, alles durch Gatter mit zwei Eingängen zu erzeugen.
Der erste Schritt dazu ist, die Schaltung auf Gattern mit zwei Eigängen beliebiger Funktion umzuwandeln. Das sähe für unseren Addierer folgendermaßen aus:
Nun kann man für die einzelnen Gatter die entsprechenden Ersatzfunktionen mit NAND's einsetzen:
-

Für die Negation die beiden Varianten 
Für die UND-Funktion 
Für die ODER-Funktion
Da der UND-Funktion oft (in unserem Fall immer) eine ODER-Funktion folg, kann man die zwei hintereinander folgenden Negatoren streichen (Negation der Negation).
Damit wird die Schaltung wesentlich einfacher (als wenn alle Gatter notwendig wären):
Ich gebe zu, es ist schon schwierig, da den Überblick zu behalten. Man muss bei der Erarbeitung ganz exakt vorgehen und keinen Fehler machen. Bevor man das mit Bausteinen aufbaut, sollte man es besser simulieren.
Man wird so eine Schaltung auch nicht aufbauen, sondern zuvor nachschauen, was schon angeboten wird und da gibt es tatsächlich einen Schaltkreis. Der 4008 ist ein 4 Bit Volladdierer (also 4 mal so eine Schaltung), so wie wir ihn oben beschrieben haben.
-

So sieht der Schaltkreis innen aus.
Auffällig ist, dass der letzte Übertrag durch eine spezielle Schaltung erzeugt wird. Das ist so bei großer Rechenbreite üblich, denn so steht der Übertrag sofort zur Verfügung.
-

Will man von diesem Schaltkreis nur einen Addierer nutzen, so geht das nur mit der letzten Stelle S4, denn nur hier erhält man auch den Übertrag Ün (C0). Bis zu dieser Stelle muss man definierte interne Überträge erzeugen, das geht immer mit 0 + 0. Für die 4. Stelle kommt also als Ü = 0. An der 4. Stelle kann man mittels Schalter die Addition überprüfen.
Aufgabe6:
Für unseren Universalbaustein zur Realisierung von 4 logischen Grundfunktionen ist eine Schaltung ausschließlich aus NAND's mit jeweils 2 Eingängen aufzubauen!
(erst einmal probieren, dann später hier nachsehen)
Nach dem wir uns nun mächtig gequält haben, auch etwas Positives.
Den Schaltkreis (in erweiterter Form) gibt es tatsächlich schon, wir können ihn
einfach nutzen - toll!
|
|
zurück zur Start-Seite |